Solving Inverse PDE Problems using Monte Carlo Estimators
1École Polytechnique Fédérale de Lausanne (EPFL), 2Google
ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia), 2024
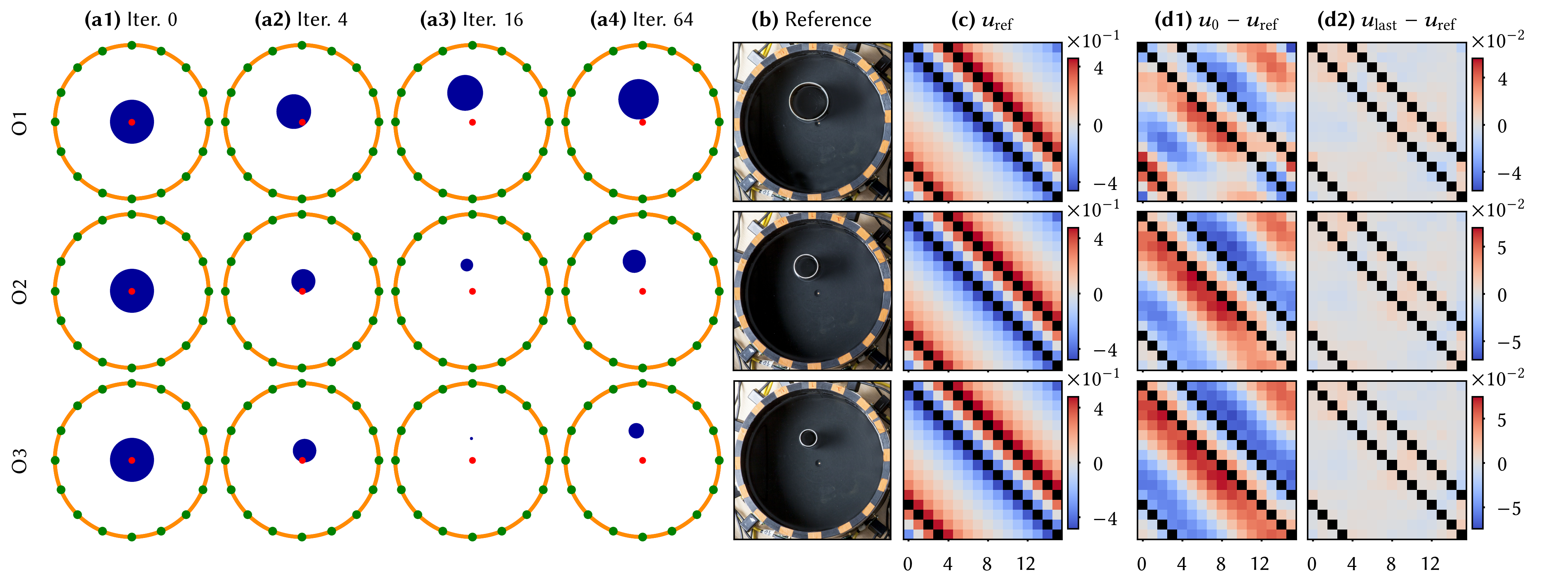
We apply our inverse PDE solver to a 2D electrical impedance tomography experiment [Hauptmann et al. 2017], in which an electric current flows through a saline-filled water tank containing conducting objects of different sizes (photographs in middle). The marker in the middle indicates the center. Injecting a current using 2 of 16 uniformly spaced electrodes at the tank boundary generates a measurable voltage difference at the other electrodes, and injecting at various locations produces a matrix 𝑢_ref of measurements. The objective of this inverse problem is to infer the properties of the conductor from this data. We perform a differentiable simulation of this setup to optimize the center and radius of a conducting circle. The frames on the left show the progression of the optimization (columns (a)), while the rightmost two columns reveal how the predicted voltages become increasingly consistent with the measurement (columns (d)).
Abstract
Partial differential equations can model diverse physical phenomena including heat diffusion, incompressible flows, and electrostatic potentials. Given a description of an object's boundary and interior, traditional methods solve such PDEs by densely meshing the interior and then solving a large and sparse linear system derived from this mesh. Recent grid-free solvers take an alternative approach and avoid this complexity in exchange for randomness: they compute stochastic solution estimates and generally bear a striking resemblance to physically-based rendering algorithms. In this article, we develop algorithms targeting the inverse form of this problem: given an already existing solution of a PDE, we infer parameters characterizing the boundary and interior. In the grid-free setting, there are again significant connections to rendering, and we show how insights from both fields can be combined to compute unbiased derivative estimates that enable gradient-based optimization. In this process, we encounter new challenges that must be addressed to obtain practical solutions. We introduce acceleration and variance reduction strategies and show how to differentiate branching random walks in reverse mode. We finally demonstrate our approach on both simulated data and a real-world electrical impedance tomography experiment, where we reconstruct the position of a conducting object from voltage measurements taken in a saline-filled tank.
Video
Downloads & resources
- Publication:
Text Reference 
Ekrem Fatih Yilmazer, Delio Vicini, Wenzel Jakob. Solving Inverse PDE Problems using Monte Carlo Estimators. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia), 43(6), December 2024.
BibTex Reference 
@article{Yilmazer2024Solving,
title = {Solving Inverse PDE Problems using Monte Carlo Estimators},
author = {Ekrem Fatih Yilmazer and Delio Vicini and Wenzel Jakob},
year = 2024,
month = dec,
journal = {Transactions on Graphics (Proceedings of SIGGRAPH Asia)},
volume = 43,
doi = {10.1145/3687990}
}